Deutsch-Jozsa algorithm

The Deutsch-Jozsa algorithm, introduced by David Deutsch and Richard Jozsa in their 1992 paper Rapid solution of problems by quantum computation, marked an important early milestone in the development of quantum algorithms. The formulation familiar to us today—featuring the standard quantum circuit model and oracle—was later refined in 1998 by Richard Cleve, Artur Ekert, Chiara Macchiavello, and Michele Mosca in their paper Quantum algorithms revisited. Both papers are highly readable, and we encourage interested readers to consult them directly.

^{Fig.1 David Deutsch(Photo Credits: Lulie Tanett, see this link) and Richard Jozsa (Photo from this link)}

As a deterministic quantum algorithm, the Deutsch-Jozsa algorithm has limited direct practical applications. Its significance lies in demonstrating, for the first time, that quantum computation can achieve an exponential speedup over all deterministic classical algorithms. Studying this algorithm offers valuable insight into how quantum algorithms are structured and why they can outperform classical methods.

It is worth noting that this exponential separation holds only when compared with deterministic classical algorithms. If classical randomness is allowed, such an exponential advantage no longer appears. The first quantum algorithm to establish an exponential speedup over any classical stochastic algorithm is Simon’s algorithm, see this post.

Definition (Problem of the Deutsch-Jozsa Algorithm). Consider a function

$f: \{0,1\}^n \to \{0,1\}$

that accepts $n$ -bit binary inputs and outputs either 0 or 1. It is guaranteed that $f$ is either constant (producing the same output for all inputs) or balanced (outputting 1 for exactly half of the inputs and $0$ for the other half). The objective is to determine whether $f$ is constant or balanced by querying the oracle.

For example, consider a one-bit input function $f: \{0,1\} \to \{0,1\}$ . The function is constant if $f(0) = f(1)$ , and balanced if $f(0) \neq f(1)$ (equivalently, $f(0) \oplus f(1) = 1$ , where $\oplus$ denotes addition modulo 2). Determining whether $f$ is constant or balanced is thus equivalent to evaluating $f(0) \oplus f(1)$ . This can also be viewed as a quantum XOR game: if the result is 0, then $f$ is constant; otherwise, $f$ is balanced.

Deutsch-Jozsa Algorithm: n=1 Case

Let us begin with the simplest example, namely the $n=1$ case of the Deutsch-Jozsa algorithm, to gain some intuition about how quantum algorithms work.

Classically, we would need to evaluate $f$ twice to solve the problem, namely compute $f(0)$ and $f(1)$ . There is no way around this. Quantum mechanically, we can do better. To begin, we need to “promote” the function $f$ to a unitary operation $U_f$ , defined by

$U_f |x\rangle |y\rangle = |x\rangle |y \oplus f(x)\rangle$

We do not concern ourselves here with how to implement $U_f$ in an actual quantum circuit. Instead, we treat it as a black box that can be used freely. Such a black box is called a quantum oracle, and we will encounter this concept frequently in many other quantum algorithms, like Simon’s algorithm, Grover search algorith, Shor’s algorithm, etc.

Exercise. As a simple practice, prove that $U_f$ defined above is a unitary operator for both balanced and constant functions $f$ .

Proof. Consider the action of $U_f$ on the four computational basis states:

$|0\rangle |0\rangle \mapsto |0\rangle |0 \oplus f(0)\rangle$

$|0\rangle |1\rangle \mapsto |0\rangle |1 \oplus f(0)\rangle$

$|1\rangle |0\rangle \mapsto |1\rangle |0 \oplus f(1)\rangle$

$|1\rangle |1\rangle \mapsto |1\rangle |1 \oplus f(1)\rangle$

Notice that $0 \oplus f(0) \neq 1 \oplus f(0)$ regardless of the value of $f(0)$ , and similarly $0 \oplus f(1) \neq 1 \oplus f(1)$ .

Hence, the images of the basis states under $U_f$ form an orthonormal basis, which shows that $U_f$ is indeed unitary. ∎

With the quantum oracle $U_f$ , the Deutsch-Jozsa algorithm works as follows.
We prepare two qubits: one for the input of $f$ and one for the output. They are initialized in the state $|0\rangle |1\rangle$ . Then we perform the following steps:

Apply Hadamard gates to both qubits: $(H \otimes H) \, |0\rangle |1\rangle$ .
Apply the oracle: $(U_f \otimes I) \big( (H \otimes H) \, |0\rangle |1\rangle \big)$ .
Apply a Hadamard gate to the first qubit: $(H \otimes I) \, (U_f \otimes I) \big( (H \otimes H) \, |0\rangle |1\rangle \big)$ .
Measure the first qubit in the computational basis.

Let us examine what happens step by step. After steps 1 and 2, we obtain

$|0\rangle |1\rangle \overset{H\otimes H}{\longrightarrow} |+\rangle |-\rangle = \frac{1}{2} \Big( |0\rangle (|0\rangle - |1\rangle) + |1\rangle (|0\rangle - |1\rangle) \Big)$

$\overset{U_f\otimes I}{\longrightarrow} \frac{1}{2}\Big( |0\rangle \big( |0 \oplus f(0)\rangle - |1 \oplus f(0)\rangle \big) + |1\rangle \big( |0 \oplus f(1)\rangle - |1 \oplus f(1)\rangle \big) \Big).$

Next, we use a simple but important trick: we rewrite the action of the oracle so that the value of $f(x)$ appears as a phase. The key identity is

$|0 \oplus z\rangle - |1 \oplus z\rangle = (-1)^z \big( |0\rangle - |1\rangle \big),$

valid for $z = 0,1$ . The state after applying the oracle can be rewritten as

$\frac{1}{2} \Big( |0\rangle (|0 \oplus f(0)\rangle - |1 \oplus f(0)\rangle) + |1\rangle (|0 \oplus f(1)\rangle - |1 \oplus f(1)\rangle) \Big)$

$= \frac{1}{2} \Big( (-1)^{f(0)} |0\rangle (|0\rangle - |1\rangle) + (-1)^{f(1)} |1\rangle (|0\rangle - |1\rangle) \Big)$

$= (-1)^{f(0)} \frac{1}{2} \Big( |0\rangle + (-1)^{f(0)\oplus f(1)} |1\rangle \Big) (|0\rangle - |1\rangle).$

Ignoring the second qubit and the global phase, the first qubit is in the state

$\frac{1}{\sqrt{2}} \Big( |0\rangle + (-1)^{f(0) \oplus f(1)} |1\rangle \Big).$

^{Fig.2 Quantum circuit for Deutsch–Jozsa algorithm (n=1 case).}

Our goal is to determine $f(0) \oplus f(1)$ , which is encoded in the relative phase $(-1)^{f(0) \oplus f(1)}$ of the first qubit. To read out this information, we apply a Hadamard gate to the first qubit and then measure it in the computational basis. This is an example of an interferometric measurement scheme, a standard method for extracting the coefficient of a state in a given basis; you will encounter this technique in many other contexts as well.

After applying the Hadamard, the state of the first qubit becomes

$\frac{1}{2} \Big( |0\rangle + |1\rangle + (-1)^{f(0)\oplus f(1)} |0\rangle - (-1)^{f(0)\oplus f(1)} |1\rangle \Big)$

$= \frac{1}{2} \Big( \big(1 + (-1)^{f(0)\oplus f(1)}\big) |0\rangle + \big(1 - (-1)^{f(0)\oplus f(1)}\big) |1\rangle \Big).$

The probabilities of measuring the first qubit in the computational basis are then

$p(0) = \frac{1}{4} \big| 1 + (-1)^{f(0) \oplus f(1)} \big|^2,$
$p(1) = \frac{1}{4} \big| 1 - (-1)^{f(0) \oplus f(1)} \big|^2.$

Hence, if $f(0)\oplus f(1) = 0$ (the function is constant), we will certainly measure $|0\rangle$ .
If $f(0)\oplus f(1) = 1$ (the function is balanced), we will measure $|1\rangle$ .

In other words, a single query to the quantum oracle suffices to determine with certainty whether $f$ is constant or balanced. In contrast, a classical algorithm would require evaluating $f$ twice.

The key mechanism at work here is quantum parallelism: in step 2, the oracle evaluates ff f across both inputs in parallel, storing the outcomes in superposition. The concluding Hadamard transformation then translates this superposed information into observable probability amplitudes, from which we can efficiently determine the answer.

Now let us turn to the general case in which $f$ has an $n$ -bit input. As in the $n = 1$ case, the classical oracle must be replaced by a quantum oracle $U_f$ that coherently evaluates the function. By definition, the quantum oracle acts as

$U_f\,|x\rangle |y\rangle = |x\rangle\, |y \oplus f(x)\rangle,$

where $x = x_1 \cdots x_n$ is an $n$ -bit string, and we write

$|x\rangle := |x_1\rangle \cdots |x_n\rangle.$

This means we use the canonical encoding that maps each bit string to a corresponding computational basis state.

Exercise. Prove that the quantum oracle $U_f$ defined by $U_f\,|x\rangle|y\rangle = |x\rangle|y\oplus f(x)\rangle$ is unitary.

Proof. The operator $U_f$ permutes the computational basis states. Indeed, for each basis vector $|x\rangle|y\rangle$ the image $|x\rangle|y\oplus f(x)\rangle$ is again a computational-basis vector, and distinct input basis vectors have distinct images because $y\mapsto y\oplus f(x)$ is a bijection on ${0,1}$. Hence the set of images of the computational basis is another orthonormal basis of the Hilbert space. A linear map that sends an orthonormal basis to an orthonormal basis preserves inner products and therefore is unitary. Thus $U_f$ is unitary (Equivalently, one can note that $U_f^2 = I$ since $(y\oplus f(x))\oplus f(x)=y$ , so $U_f$ is invertible with $U_f^{-1}=U_f$ , and a permutation matrix with real entries has its inverse equal to its adjoint; either way $U_f$ is unitary.) ∎

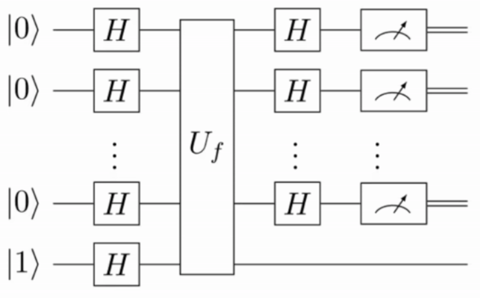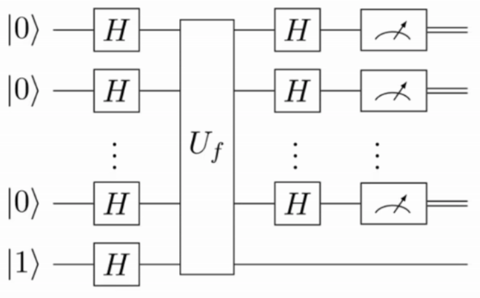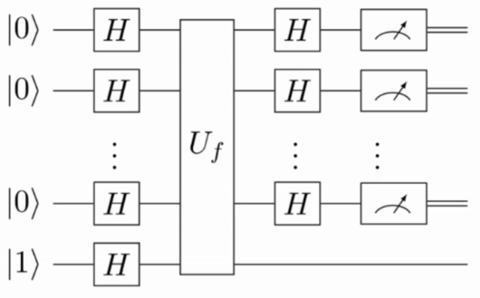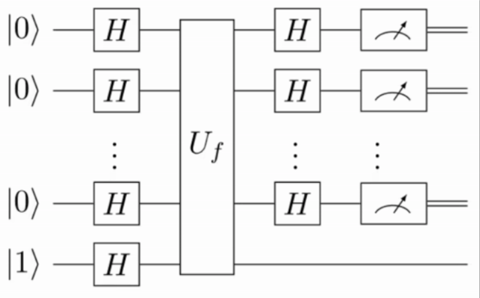
The quantum circuit for the Deutsch–Jozsa algorithm is shown in Figure 3. The algorithm proceeds as follows:

Initial State: Prepare an n-qubit input register in the state $|0\rangle^{\otimes n}$ and a single output qubit in the state $|1\rangle$ :
$|0\rangle^{\otimes n} \otimes |1\rangle$ .
Hadamard Transform: Apply the Hadamard gate to each qubit:
$\frac{1}{\sqrt{2^n}} \sum_{x \in \{0,1\}^n} |x\rangle \otimes \frac{1}{\sqrt{2}} (|0\rangle - |1\rangle)$ .
Oracle Query: Apply the quantum oracle $U_f$ :
$U_f |x\rangle |y\rangle = |x\rangle |y \oplus f(x)\rangle$ .
After applying the oracle, the state becomes
$\frac{1}{\sqrt{2^n}} \sum_{x \in \{0,1\}^n} (-1)^{f(x)} |x\rangle \otimes \frac{1}{\sqrt{2}} (|0\rangle - |1\rangle)$ ,
using the identity
$|0 \oplus f(x)\rangle - |1 \oplus f(x)\rangle = (-1)^{f(x)} (|0\rangle - |1\rangle)$ .
The output qubit is no longer entangled with the input register, so we can ignore it, leaving
$\frac{1}{\sqrt{2^n}} \sum_{x \in \{0,1\}^n} (-1)^{f(x)} |x\rangle$ .
Second Hadamard Transform: Apply $H^{\otimes n}$ to the input register:
$H^{\otimes n} |x\rangle = \frac{1}{\sqrt{2^n}} \sum_{z \in \{0,1\}^n} (-1)^{x \cdot z} |z\rangle$ ,
giving
$\frac{1}{2^n} \sum_{z \in \{0,1\}^n} \left( \sum_{x \in \{0,1\}^n} (-1)^{f(x) + x \cdot z} \right) |z\rangle$ .
Measurement: Measure the n-qubit input register. The outcome reveals the type of function:

If $f$ is constant, interference ensures only $|0\rangle^{\otimes n}$ appears.
If $f$ is balanced, destructive interference prevents $|0\rangle^{\otimes n}$ from appearing.

Measuring $|0\rangle^{\otimes n}$ indicates a constant function; any other outcome indicates a balanced function.

Exercise: Verify that the states at each step of the n-qubit Deutsch-Jozsa algorithm match the evolution described above for a given function $f$ .

Classically, if we want to solve the problem by brute force, we need to check about half of the inputs, thus evaluating $f$ up to $2^{n-1}$ times in the worst case. The Deutsch-Jozsa algorithm solves the problem with only one evaluation of the oracle, compared to the exponentially growing number of evaluations required by a classical algorithm. The quantum algorithm achieves this exponential speedup by leveraging quantum superposition and interference.

M	T	W	T	F	S	S
						1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28