The order-finding problem is a fundamental problem that plays a central role in several quantum algorithms; in particular, it underlies Shor’s celebrated factoring algorithm. Classically, order-finding is hard—no efficient classical algorithm is known—but quantum computers can solve it efficiently. Efficiently determining the order of an integer modulo  allows integers to be factored in polynomial time, which would compromise RSA encryption, as we will discuss in the subsequent sections.
allows integers to be factored in polynomial time, which would compromise RSA encryption, as we will discuss in the subsequent sections.
The order-finding problem is defined rigorously as follows:
At first glance, this definition may appear somewhat abstract.
Do not worry—shortly, we will unpack each of the mathematical ingredients and illustrate their meaning with concrete examples.
The quantum algorithm for order-finding exploits the periodic structure of the function

which is periodic with period exactly  . By preparing a quantum superposition over all possible exponents and applying the quantum phase estimation algorithm to the unitary operator
. By preparing a quantum superposition over all possible exponents and applying the quantum phase estimation algorithm to the unitary operator

we obtain an efficient quantum procedure that succeeds with high probability.
Preliminaries of Modular Arithmetic
Before presenting the complete quantum algorithm, let us first review a few essential results from number theory. This section may appear somewhat technical compared to others; if you prefer not to delve into the details, simply remember that for coprime integers  and
and  , there exists a positive order
, there exists a positive order  , and the function in Eq.(1) is periodic and turn to the next section.
, and the function in Eq.(1) is periodic and turn to the next section.
An integer  is called a prime number if it has no nontrivial divisors; for example,
is called a prime number if it has no nontrivial divisors; for example,  are prime numbers. Otherwise,
are prime numbers. Otherwise,  is called a composite number. We use
is called a composite number. We use 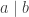 to denote that
to denote that  is divisible by
is divisible by  , for instance
, for instance  ,
,  . Similarly,
. Similarly,  means that
means that  does not divide
does not divide  , for example
, for example  .
.
Every integer  can be uniquely expressed as a product of prime powers:
can be uniquely expressed as a product of prime powers:

where  are distinct prime numbers and
are distinct prime numbers and  are positive integers. This result is known as the Fundamental Theorem of Arithmetic.
are positive integers. This result is known as the Fundamental Theorem of Arithmetic.
To obtain the prime factorization of a given number  , one typically follows these steps:
, one typically follows these steps:
- Divide
 by
by  repeatedly until the quotient is no longer divisible by
repeatedly until the quotient is no longer divisible by  .
.
Let 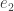 be the number of times we divide by
be the number of times we divide by  , and denote the resulting quotient by
, and denote the resulting quotient by  , for which
, for which  .
.
- For the quotient
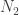 , proceed with the next prime,
, proceed with the next prime, 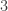 , and divide repeatedly until the quotient is no longer divisible by
, and divide repeatedly until the quotient is no longer divisible by 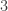 .
.
Let 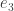 be the number of divisions, and denote the resulting quotient by
be the number of divisions, and denote the resulting quotient by  .
.
- Continue in this manner with successive primes
 until the quotient becomes
until the quotient becomes  .
.
Exercise. Decompose  into its prime factors:
into its prime factors:  .
.
The key operation we will use is modular arithmetic.
In everyday life we count linearly: 1, 2, 3, …, but in modular arithmetic we count on a circle.
Take a clock that shows only 12 hours. When the hand reaches 12, it jumps back to 0.
Mathematically, we say time is measured modulo 12.
This simple idea—wrapping around after a fixed modulus  —is crucial in number theory and its applications in modern public-key cryptography.
—is crucial in number theory and its applications in modern public-key cryptography.
Definition (Congruence) Fix an integer  , called the modulus.
, called the modulus.
Two integers  and
and  are congruent modulo
are congruent modulo  if their difference is a multiple of
if their difference is a multiple of  :
:

We read  as “
as “ is congruent to
is congruent to  modulo
modulo  ”.
”.
The congruence class of  is usually represented by its smallest non-negative residue:
is usually represented by its smallest non-negative residue:

It is also convenient to use ![[a]](https://s0.wp.com/latex.php?latex=%5Ba%5D&bg=ffffff&fg=333333&s=0&c=20201002) to denote the congruence class whenever there is no ambiguity about the modulus.
to denote the congruence class whenever there is no ambiguity about the modulus.
Example. Let 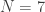 . We have
. We have  . Then
. Then  and
and  . The congruence class
. The congruence class ![[0]](https://s0.wp.com/latex.php?latex=%5B0%5D&bg=ffffff&fg=333333&s=0&c=20201002) consists of
consists of  , the congruence class
, the congruence class ![[1]](https://s0.wp.com/latex.php?latex=%5B1%5D&bg=ffffff&fg=333333&s=0&c=20201002) consists of
consists of  , and
, and ![[2]](https://s0.wp.com/latex.php?latex=%5B2%5D&bg=ffffff&fg=333333&s=0&c=20201002) consists of
consists of  , etc.
, etc.
The order-finding problem considers the modular exponentiation for given integers  and
and  :
:

The remainder  can take values in
can take values in  :
:



However, not all values of  are necessarily attainable.
are necessarily attainable.
For example, let 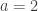 and
and  . We find that
. We find that






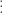
We observe a repeating pattern. In this case, the residues  ,
, 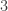 , and
, and 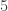 never appear.
never appear.
Note also that  for any integers
for any integers  and
and  . Hence, the order of
. Hence, the order of  modulo
modulo  is defined as the smallest positive integer
is defined as the smallest positive integer  such that
such that  . However, we must still ensure that such an order actually exists. In fact, if
. However, we must still ensure that such an order actually exists. In fact, if  , then no positive integer
, then no positive integer  satisfies
satisfies  . This can be seen in the previous example with
. This can be seen in the previous example with 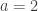 and
and  , where the sequence never returns to
, where the sequence never returns to  modulo
modulo  .
.
Exercise. Let  and
and  . Then the only integer
. Then the only integer  satisfying
satisfying

is 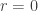 .
.
Proof. Suppose there exists an integer  such that
such that  .
.
Then  divides
divides  , so in particular
, so in particular
 .
.
Since  , we also have
, we also have  , and therefore
, and therefore
 ,
,
which contradicts 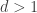 . Hence no such
. Hence no such  exists.
exists.
For 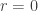 , the convention
, the convention  gives
gives

trivially. Thus 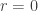 is the only solution ∎.
is the only solution ∎.
In Shor’s algorithm, we either assume  , or first compute the greatest common divisor classically, which already yields a nontrivial factor of
, or first compute the greatest common divisor classically, which already yields a nontrivial factor of  if
if 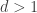 .
.
Another useful concept we will use is Euler’s Totient function: 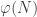 counts the number of integers
counts the number of integers  coprime to
coprime to  .
.
For example,  ,
,  ,
,  ,
,  , etc.
, etc.
For fixed  , consider
, consider  .
.
We call  invertible if there exists an integer
invertible if there exists an integer  such that
such that  .
.
Proposition (Bézout’s Identity). Let  and
and  be integers with greatest common divisor
be integers with greatest common divisor  . Then there exist integers
. Then there exist integers  and
and  such that
such that
 .
.
Moreover, the integers of the form  are exactly the multiples of
are exactly the multiples of  .
.
The set  is not a group under multiplication modulo
is not a group under multiplication modulo  in general. We denote by
in general. We denote by  the set of invertible elements, which indeed forms a group. By Bézout’s identity,
the set of invertible elements, which indeed forms a group. By Bézout’s identity,  consists of all integers coprime to
consists of all integers coprime to  , and this group has order
, and this group has order  , where
, where  denotes Euler’s totient function.
denotes Euler’s totient function.
From a group-theoretic perspective, for any  , there exists a positive integer
, there exists a positive integer  such that
such that
 .
.
Since  must be invertible, it follows that
must be invertible, it follows that  . In the multiplicative group
. In the multiplicative group  , the order of any element divides the order of the group, that is,
, the order of any element divides the order of the group, that is,
 .
.
Theorem (Euler’s Theorem). If  , then
, then

and hence the order of  modulo
modulo  divides
divides  .
.
By Euler’s theorem, for integers  and
and  with
with  , there always exists a positive integer
, there always exists a positive integer  such that
such that

The order  always satisfies
always satisfies  .
.
Since in the cyclic subgroup generated by ![[a] \in \mathbf{Z}_N^{\times}](https://s0.wp.com/latex.php?latex=%5Ba%5D+%5Cin+%5Cmathbf%7BZ%7D_N%5E%7B%5Ctimes%7D&bg=ffffff&fg=333333&s=0&c=20201002) we have
we have
![{[a^0], [a^1], [a^2], \dots, [a^{r-1}]}, \quad \text{with } [a^r] = [a^0] = [1],](https://s0.wp.com/latex.php?latex=%7B%5Ba%5E0%5D%2C+%5Ba%5E1%5D%2C+%5Ba%5E2%5D%2C+%5Cdots%2C+%5Ba%5E%7Br-1%7D%5D%7D%2C+%5Cquad+%5Ctext%7Bwith+%7D+%5Ba%5Er%5D+%3D+%5Ba%5E0%5D+%3D+%5B1%5D%2C&bg=ffffff&fg=333333&s=0&c=20201002)
the sequence  is periodic with period equal to the order
is periodic with period equal to the order  :
:








Thus, the sequence repeats with period  .
.
Example. Set 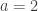 and
and 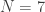 . We have
. We have  as:
as:









We see that the order is  .
.
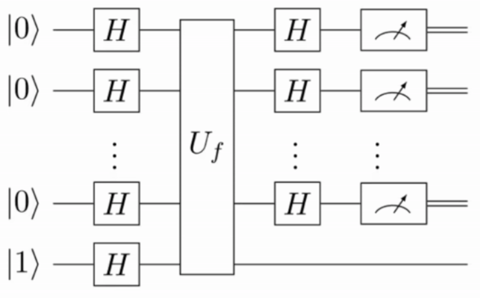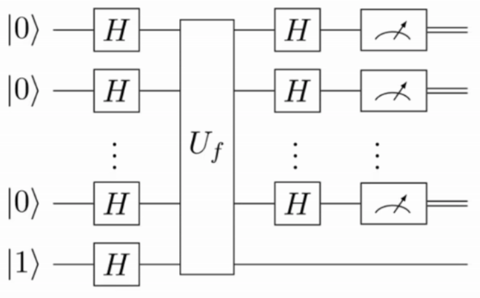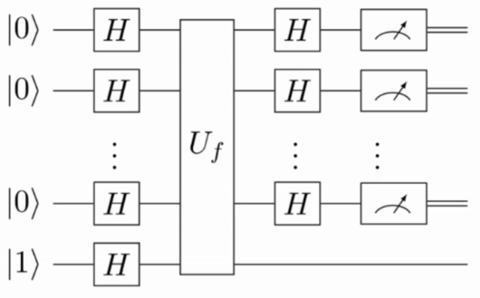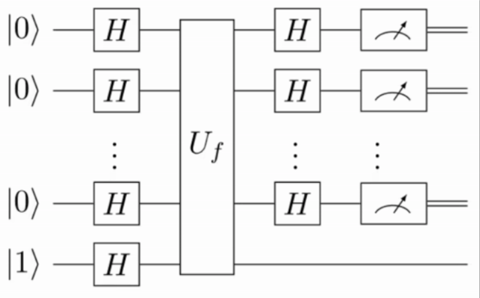
Quantum Order-Finding Algorithm
The quantum order-finding algorithm can be divided into two main steps:
- Encode the order into the phase of an eigenvalue of a suitable unitary operator, thereby reducing the order-finding problem to a quantum phase estimation problem.
- Recover the order
 from the estimated phase
from the estimated phase 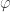 using the method of continued fractions.
using the method of continued fractions.
Let us first examine how to encode the order into the phase of a unitary operator.
Fix integers  and
and  such that
such that  .
.
Define the unitary operator  acting on computational basis states
acting on computational basis states  by
by

We will see that the order can be mapped to the phase of an eigenvalue of  .
.
Proposition. Let  and let
and let  be an integer coprime to
be an integer coprime to  .
.
The operator  on
on  defined by
defined by

is unitary.
Proof. Since  , multiplication by
, multiplication by  modulo
modulo  defines a bijection on the set
defines a bijection on the set  .
.
Thus  merely permutes the computational basis
merely permutes the computational basis  . Any permutation of an orthonormal basis extends to a unitary operator, so
. Any permutation of an orthonormal basis extends to a unitary operator, so  is unitary.
is unitary.
Alternatively, suppose  . Then
. Then
 .
.
Because  , we may cancel
, we may cancel  (more precisely, multiply both sides by the modular inverse of
(more precisely, multiply both sides by the modular inverse of  modulo
modulo  ) to obtain
) to obtain
 .
.
Since  , the only possibility is
, the only possibility is  , so
, so  .
.
Thus  is injective on a basis of
is injective on a basis of  .
.
Being an isometry that maps a basis to a basis, it is unitary ∎.
Proposition. Let  be the order of
be the order of  modulo
modulo  , i.e., the smallest positive integer such that
, i.e., the smallest positive integer such that
 .
.
For each  , define the state
, define the state

Then, for each  ,
,  is an eigenstate of
is an eigenstate of  with eigenvalue
with eigenvalue
 .
.
Proof. Apply  to
to  :
:


Reindex the sum by letting  :
:



The sum now runs from 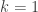 to
to  , but the
, but the  term is
term is

while the 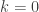 term in the original definition of
term in the original definition of  is
is

Thus the missing 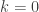 term is exactly replaced by the
term is exactly replaced by the  term, and we obtain
term, and we obtain

This holds for every  ∎.
∎.
Now the procedure becomes “straightforward”. We apply quantum phase estimation (see this post) to the operators  with the eigenstate
with the eigenstate  , which yields the phases
, which yields the phases

The output of the phase estimation algorithm is thus

represented as binary numbers. A classical algorithm called continued fractions can be applied to obtain the order  .
.
. We also prove the Haag duality for the gound state of color code model.